The term “nutritional anthropometry” first appeared in “Body Measure­ments and Human Nutrition” (Brožek, 1956) and was later defined by Jelliffe (1966) as:

“mea­sure­ments of the variations of the physical dimensions and the gross composition of the human body at different age levels and degrees of nutrition”

Subsequently, a number of publications made recom­mendations on specific body mea­sure­ments for characterizing nutri­tional status, standardized mea­sure­ment techniques, and suitable reference data (Jelliffe, 1966; WHO, 1968; Weiner and Lourie, 1969). Today, anthro­pometric mea­sure­ments are widely used for the assessment of nutri­tional status and health, at both the individual and population levels. One of their main advantages is that anthro­pometric mea­sure­ments may be related to past exposures, to present processes, or to future events (WHO, 1995).

For individuals in low-income countries, anthro­pometry is partic­ularly useful when there is a chronic imbalance between intakes of energy, protein, and certain micronutrients. Such disturbances modify the patterns of physical growth and the relative proportions of body tissues such as fat, muscle, and total body water. For individuals in clinical settings, anthro­pometry can be used to diagnose failure to thrive in infants and young children, and monitor over­weight and obesity in children and adults.

At the population level, anthro­pometry has an important role in targeting inter­ventions through screening, in assessing the response to inter­ventions, in identi­fying the deter­minants and consequences of mal­nu­trition, and in conducting nutri­tional surveillance. Increasingly, anthro­pometry is also being used to characterize and compare the health and nutri­tional status of populations across countries (WHO/UNICEF, 2019).

9.1 Mea­sure­ments, indices, and indicators

Anthro­pometric mea­sure­ments are of two types. One group of mea­sure­ments assesses body size, the other group appraises body composition. The most widely used mea­sure­ments of body size are stature (length or height), weight, and head circum­ference; see Chapter 10 for more details. The anthro­pometric mea­sure­ments of body composition are based on the classical “two component model” in which the body is divided into two major compartments, fat mass and the fat free mass. Skinfold thickness mea­sure­ments are used to estimate of the size of the sub­cu­taneous fat depot, which, in turn provides an estimate of total body fat: over one third of total body fat is estimated to be sub­cu­taneous fat. The distri­bution of body fat is also important, with the mea­sure­ment of waist circum­ference used increasingly as a proxy for the amount of intra-abdominal visceral fat. Waist circum­ference is recom­mended for use in population studies (WHO, 2011), as well as in clinical practice for the evaluation and management of patients with over­weight or obesity (Ross et al., 2020).

The fat-free mass consists of the skeletal muscle, non-skeletal muscle, soft lean tissue, and the skeleton. A major component of the fat-free mass is body muscle. As this is composed of protein, assessment of muscle mass can provide an indirect assessment of the protein reserves of the body. Measure­ments of thigh circum­ference and mid-upper-arm circum­ference (MUAC) can be used to assess skeletal muscle mass (Müller et al., 2016). Measure­ment of MUAC is especially useful for young children < 5y in emergency settings such as famines and refugee crises. In such settings, children often have a small amount of sub­cutan­eous fat, so changes in MUAC tend to parallel changes in muscle mass; see Chapter 11 for more details.

Anthro­pometric indices are usually calculated from two or more raw mea­sure­ments, and are essential for the inter­pretation and grouping of mea­sure­ments collected in nutri­tional assessment. For example, the mea­sure­ment of a child's body weight is meaningless unless it is related to the age or height of a child. In young children the three most commonly used growth indices are weight-for-age, height-for-age, and weight-for-height. The first two indices reflect body weight or height relative to chronological age, whereas weight-for-height assesses body weight relative to height.

Body mass index (BMI) is also widely used in children and adults to assess under­weight, over­weight, and obesity, and is calculated as (weight kg) / (height m)². When height cannot be measured, as may occur in bed-bound or frail individuals, published equations based on a range of body mea­sure­ments such as knee height, lower leg length, arm span, and ulna length can be used to provide an approximate estimate of height. Examples of equations for estimating height from these body mea­sure­ments in adults are given in Madden et al. (2016). However, their usefulness for hospitalised patients may be questionable, if the equations have been derived from young and healthy populations (Reidlinger et al., 2014).

Examples of body composition indices include a combination of triceps skinfold and mid-upper-arm circum­ference, which together can be used to estimate mid-upper-arm fat area and mid-upper-arm muscle circum­ference or area, surrogates for total body fat content, and muscle mass, respectively. Other mea­sure­ment combinations include the waist-hip ratio (i.e., the waist circum­ference divided by the hip circum­ference), an additional index of the distri­bution of body fat which can be measured more precisely than skinfolds. Moreover, mea­sure­ments of waist-hip ratio as a surrogate for abdominal obesity, appear to be a stronger inde­pen­dent risk factor for risk of myocardial infarction, stroke and premature death than BMI, especially among men (Larsson et al., 1984; Lapidus et al., 1984).

In an effort to obtain more reliable estimates of per­cent­age body fat and fat-fat-free mass based on anthro­pometric mea­sure­ments in healthy adults, the sum of skinfold thickness mea­sure­ments from multiple anatomical sites is also used in conjunction with population-specific or generalized regression equations to predict body density, and in turn, the per­cent­age of body fat using one of three empirical equations. Once the per­cent­age of body fat is calculated, total body fat content and the fat-free mass can be derived (see Chapter 11 for more details). Again, many of the prediction equations were developed on young, healthy, lean Caucasian population groups and, hence, are less appro­priate for malnourished, obese, or elderly subjects or for other racial groups.

Anthropometric indices are often evaluated by comparison with the distri­bution of appro­priate anthropometric reference data using standard deviation scores (Z‑scores) or per­cen­tiles. (see Section 9.4.3). From this, the number and proportion of individuals (as %) with anthropometric indices below or above a predetermined reference limit or cutoff are often calculated. A commonly used reference limit for the three main growth indices is a Z‑score of −2 (i.e., below the WHO reference median) (Section 9.4.2). When used in this way, the index and its associated reference limit or cutoff become an “indicator”; these are discussed below.

Anthro­pometric indicators are constructed from anthro­pometric indices, with the term “indicator” relating to their use in nutri­tional assessment, often for public health, or socio-medical decision-making at the population level. Indicators are also used in clinical settings to identify individuals at risk of malnutrition. To be valid, a substantial proportion of the variability of an anthro­pometric indicator should be associated with differences in nutri­tional status. WHO (1995) provide a detailed classification of recom­mended anthro­pometric indicators based on their uses for both targeting and assessing response to inter­ventions, identi­fying deter­minants of mal­nu­trition, or predicting mal­nu­trition in populations of infants and children.

Anthro­pometric indicators should be chosen carefully in relation to both their proposed use and their attributes. Indicators vary in their validity, sensitivity, specificity, and predictive value; these characteristics are discussed briefly in Section 9.4.3. For example, although the indicator weight-for-age < −2 Z‑score is still widely used in health centers in many low-income countries for screening young children at risk of malnutrition, it is inappro­priate. Children who are stunted but of normal weight, or alternatively, tall and thin may be incorrectly diagnosed as “healthy”. Instead, in these countries, the indicator length/height-for-age < −2 Z‑score should be used (Ruel et al., 1995).

Table 9.1 Anthropometric indicators and their corresponding applications.

Anthro­pometric indicator	Application
Proportion of children (of defined      age and sex) with WHZ < −2	Prevalence of wasting
Proportion of children (of defined      age and sex) with HAZ < −2	Prevalence of stunting
Proportion of children (of defined      age and sex) with WAZ < −2	Prevalence of under­weight
Proportion of children 0–5y (of defined age      and sex) with BMIZ > +2 or BMIZ > +3	Prevalence of over­weight or obesity
Proportion of adult women or men with waist-      hip ratios > 0.85 (F) and > 0.90 (M)	Prevalence of abdominal obesity and      thus risk of metabolic syndrome
Proportion of children 6–60mos       with MUAC < 115mm	Prevalence of severe acute      mal­nu­trition (SAM)
Proportion of children with SAM who have      MUAC > 125mm and no edema for at least      2wk after receiving treatment for SAM	Prevalence of children ready for dis-      charge following treatment for SAM

Further, several factors will affect the magnitude of the expected response of an anthropometric indicator. These may include the degree of defi­ciency, age, sex, and physiological state of the target group. Some examples of frequently used anthro­pometric indicators and their corresponding application are shown in Table 9.1.

9.2 Advantages and limitations of anthro­pometry

Anthro­pometric mea­sure­ments are of increasing importance in nutri­tional assessment as they have many advantages (Box 9.1). However, anthro­pometric measures are relatively insensitive and cannot detect disturbances in nutri­tional status over short periods of time. Further­more, nutri­tional anthro­pometry cannot identify any specific nutrient defi­ciency and, therefore, is unable to distinguish disturbances in growth and body composition induced by nutrient deficiencies (e.g., zinc) from those caused by imbalances in protein and energy intake.

Certain non-nutri­tional factors (such as disease, genetic influences, diurnal variation, and reduced energy expenditure) can lower the specificity and sensitivity of anthro­pometric mea­sure­ments (Section 1.4), although such effects generally can be excluded or taken into account by appro­priate sampling and experi­mental design.

Nevertheless, nutri­tional anthro­pometry can be used to monitor changes in both growth and body compo­sition in individuals (e.g., hospital patients) and in population groups, provided sources of mea­sure­ment error and the effects of confounding factors are minimized (Ulijaszek & Kerr, 1999).

9.3 Errors in anthro­pometry

Errors can occur in nutri­tional anthro­pometry which may affect the precision, accuracy, and validity of the mea­sure­ments, and thus indices and indicators. Three major sources of error are significant: mea­sure­ment errors, alterations in the compo­sition and physical properties of certain tissues, and the use of invalid assumptions in the derivation of body compo­sition from anthro­pometric mea­sure­ments (Heymsfield and Casper, 1987).

Measure­ment errors arise from examiner error resulting from inadequate training, instru­ment error, and difficulties in making the mea­sure­ment (e.g., skinfold thicknesses). The major sources of mea­sure­ment error in anthro­pometry are shown in Boxes 9.2 and 9.3. Both random and sys­tem­atic mea­sure­ment errors may occur which reduce the validity of the index and any indicator constructed from the index; they have been extensively reviewed by Ulijaszek and Kerr (1999).

9.3.1 Random mea­sure­ment errors and precision

Random mea­sure­ment errors limit precision or the extent to which repeated mea­sure­ments of the same variable give the same value. Random mea­sure­ment errors can be minimized by training personnel to use standardized techniques and precise, correctly calibrated instru­ments (Lohman et al., 1988) . Further­more, the precision (and accuracy) of each mea­sure­ment technique should be firmly established prior to use. To improve precision, two or three mea­sure­ments on each individual should be conducted.

A description of the mea­sure­ment techniques used in the WHO Multi­center Growth Reference Study (MGRS) are available in de Onis et al. (2004), as well as in an anthro­pometric training video from WHO. In the WHO MGRS the equipment was calibrated regularly, using standard weights over the full weight range for the portable electronic weighing scales, metal rods of known length for both the infantometer and stadiometer, and calibration blocks of varying widths for the skinfold calipers.

Poor precision often reflects within-examiner error, but between-examiner error may also be significant in surveys with multiple examiners. The precision of a mea­sure­ment technique can be assessed by calculating:

• Technical error of the mea­sure­ment (TEM)
• per­cent­age technical error (%TEM)
• Coefficient of reliability (R)

These parameters can be calculated for each anthro­pometric mea­sure­ment technique from repeated mea­sure­ments on each subject made within a few minutes to avoid physiological fluctuations. A minimum of 10 subjects is recom­mended. The technical error of the mea­sure­ment (TEM) is the square root of the mea­sure­ment error variance. TEM is expressed in the same units as that of the anthro­pometric mea­sure­ment under study and is often age dependent. The value is also related to the anthro­pometric characteristics of the study group. The calculation varies according to the number of replicate mea­sure­ments made. 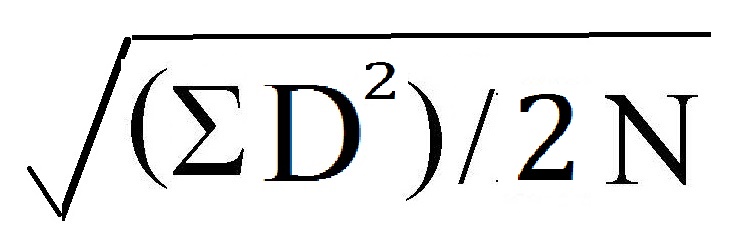For one examiner making two mea­sure­ments, TEM = where D = the difference between two mea­sure­ments and N = number of subjects. For more than two mea­sure­ments, the equation is more complex, and TEM = 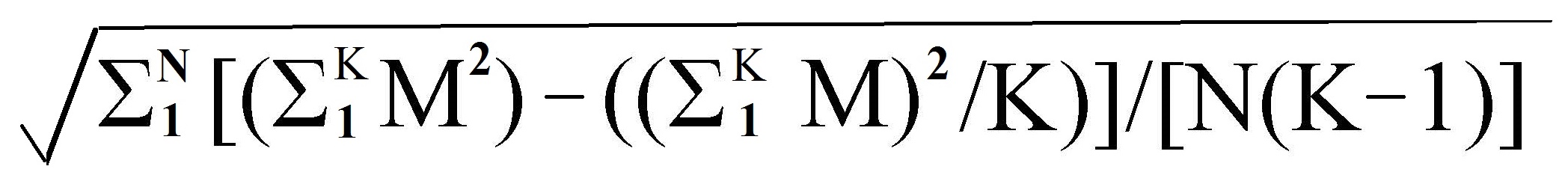where N = number of subjects, K is the number of deter­minations of the variable taken on each subject, and M_n is the n^th replicate of the mea­sure­ment, where n varies from 1 to K.

Table 9.2:

Table 9.2 Sample calculation of technical error of mea­sure­ment (TEM) from repeat mea­sure­ments of stature (m) carried out by one anthro­pometrist on 10 subjects. M= mea­sure­ment, K= number of replicates, N= number of subjects.

Subject	Stature (m) as deter­mined on repeat				(1)	(2)	Diff.
no.	1	2	3	4	ΣM2	(ΣM)2/K	(1) − (2)
1	0.865	0.863	0.863	0.864	2.984259	2.984256	0.000003
2	1.023	1.023	1.027	1.025	4.198412	4.198401	0.000011
3	0.982	0.980	0.989	0.985	3.873070	3.873024	0.000046
4	0.817	0.816	0.812	0.817	2.660178	2.660161	0.000017
5	0.901	0.894	0.900	0.903	3.236446	3.236401	0.000045
6	0.880	0.876	0.881	0.881	3.094098	3.094081	0.000017
7	0.948	0.947	0.947	0.946	3.587238	3.587236	0.000002
8	0.906	0.905	0.907	0.908	3.286974	3.286969	0.000005
9	0.924	0.924	0.926	0.924	3.418804	3.418801	0.000003
10	0.969	0.987	1.002	0.993	3.942343	3.942210	0.000133
							Σ = 0.000282
TEM = $\sqrt{\mathrm{0.000282/[N(K\; -\; 1)]}}$ = $\sqrt{\mathrm{0.000282/[10(4\; -\; 1)]}}$ = 0.00307

shows the calculation of TEM from mea­sure­ments of stature performed four times on 10 subjects by a single anthro­pometrist.

Note that the size of the mea­sure­ment also influences the size of the associated TEM, so that comparisons of precision of different anthro­pometric mea­sure­ments using TEM cannot be made easily. This is high­lighted in Table 9.3 in which the TEM for five anthro­pometric mea­sure­ments taken during the initial standardization session conducted at the Brazilian site of the WHO Multi­centre Growth Reference Study (MGRS) are presented (de Onis et al., 2004). Table 9.3 also depicts the maximum allowable differences between the mea­sure­ments of two observers that were used in the WHO MGRS, and set based on TEMs achieved during the standardization session.

Table 9.3. Maximum allowable differences between the mea­sure­ments of two observers.
TEM: Technical error of mea­sure­ment
From: de Onis et al., 2004.

mea­sure­ment	Brazil TEM from pilot study	Maximum allowable difference
Weight	Not available	100g
Length	2.5mm	7.0mm
Head circum­ference	1.4mm	5.0mm
Arm circum­ference	1.8mm	5.0mm
Triceps skinfold	0.44mm	2.0mm
Subscapular skinfold	0.43mm	2.0mm

Per­cent­age TEM has been recom­mended to overcome the difficulty of the TEM being dependent on the size of the original mea­sure­ment (Norton and Olds, 1996). The per­cent­age technical error of the mea­sure­ment is analogous to the coefficient of variation and is calculated as: \[\small\mbox{%TEM = (TEM/mean) × 100% } \] Note that %TEM has no units and can be used to make direct comparisons of all types of anthro­pometric mea­sure­ments. It cannot be used, however, when more than one examiner is involved, as then both within- and between-examiner errors are involved. Ulijaszek and Kerr (1999) describe ways to deal with this more complex case.

The coefficient of reliability (R) is an alternative approach that is widely used for comparing mea­sure­ment errors among anthro­pometric mea­sure­ments. It ranges from 0 to 1 and can be calculated using the following equation: \[\small\mbox{ R = 1 −((TEM)}^{2}/ \mbox{s} ^{2}) \] where s² is the between-subject variance. The coefficient indicates the proportion of between-subject variance in a measured population which is free from mea­sure­ment error. Hence, a mea­sure­ment with R = 0.95 indicates that 95% of the variance is due to factors other than mea­sure­ment error.

Whenever possible, a coefficient of reliability > 0.95 should be sought. Coefficients of reliability can be used to compare the relative reliability of different anthro­pometric mea­sure­ments, and the same mea­sure­ments in different age groups, as well as for calculating sample sizes in anthro­pometric surveys.

More details of standardization procedures and calculation of precision using TEM, per­cent­age TEM, and coefficient of reliability are given in Lohman et al. (1988). In general, the precision of weight and height mea­sure­ments are high. However, for waist and hip circum­ferences, between-examiner error tends to be large and it is preferable for only one examiner to take these mea­sure­ments. Because skinfolds are notoriously imprecise, both within- and between-examiner errors can be large. Therefore, rigorous training using standardized techniques and calibrated equipment are critical when skinfold mea­sure­ments are taken.

9.3.2. Sys­tem­atic mea­sure­ment errors and accuracy

Sys­tem­atic mea­sure­ment errors affect the accuracy of anthro­pometric mea­sure­ments or how close the mea­sure­ments are to the true value. The most common form of sys­tem­atic error in anthro­pometry results from equipment bias. For example, apparent discrepancies in skinfold mea­sure­ments performed on the same person but with different calipers may be due to compression differences arising from variations in spring pressure and surface area of the calipers (Schmidt & Carter, 1990); Harpenden and Holtain skinfold calipers consistently yield smaller values than Lange calipers (Gruber et al., 1990). Errors arising from bias reduce the accuracy of the mea­sure­ment by altering the mean or median value, but have no effect on the variance. Hence, such errors do not alter the precision of the mea­sure­ment.

The timing of some anthro­pometric mea­sure­ments of body size and compo­sition is also known to be critical, partic­ularly for short-term growth studies: progressive decreases in the height of an individual during the day as a consequence of compression of the spinal column, for example, may seriously compromise the accuracy of height velocity mea­sure­ments.

The deter­mination of accuracy in anthro­pometry is difficult because the correct value of any anthro­pometric mea­sure­ment is never known with absolute certainty. In the absence of absolute reference standards, the accuracy of anthro­pometric mea­sure­ments is estimated by comparing them with those made by a criterion anthro­pometrist (Ulijaszek & Kerr, 1999), a person who has been highly trained in the standardized mea­sure­ment techniques and whose mea­sure­ments compare well to those from another criterion anthro­pometrist.

In preparation for the compilation of the new WHO Child Growth Standard, four anthro­pometrists were trained and standardized against a criterion anthro­pometrist, designated as the “lead” anthro­pometrist; see de Onis et al. (2004) for more details. All anthro­pometric mea­sure­ments were taken and recorded inde­pen­dently by two designated anthro­pometrists, and their mea­sure­ment values compared for maximum allowable differences (Table 9.3). Targets for sports anthro­pometrists are also available (Gore et al., 1996).

Attempts should always be made to minimize mea­sure­ment errors. In longitudinal studies involving sequential anthro­pometric mea­sure­ments on the same group of individuals (e.g., surveillance), it is preferable, whenever possible, to have one person carrying out the same mea­sure­ments throughout the study to eliminate between-examiner errors. This is partic­ularly critical when increments in growth and body compo­sition are calculated; such increments are generally small and are associated with two error terms, one on each mea­sure­ment occasion. Recom­mendations for the minimum intervals necessary to provide reliable data on growth increments during infancy and early childhood (Guo et al., 1991) and adolescence (WHO, 1995) are available.

In large regional surveillance studies, it is often necessary to use several well-trained anthro­pometrists. In such circumstances, the between-examiner differences among anthro­pometrists must be monitored throughout the study to maintain the quality of the mea­sure­ments and thereby to identify and correct sys­tem­atic errors in the mea­sure­ments. This practice was followed during the WHO MGRS (de Onis et al., 2004).

In studies involving two longitudinal mea­sure­ments, the TEM can be calculated to estimate the proportion of the difference that can be attributed to mea­sure­ment error. For example, with a TEM of 0.3 for a given anthro­pometric mea­sure­ment, the TEM for the difference between two mea­sure­ments is: 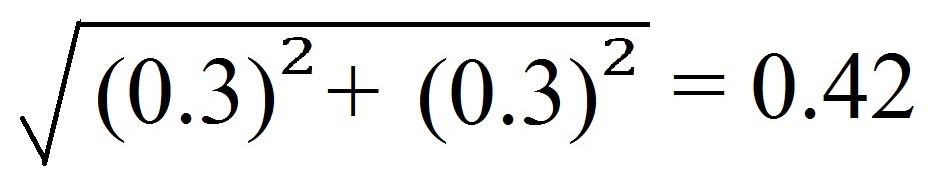because both TEM values contribute to the variance in the difference. Only if the difference exceeds 2 × 0.42 = 0.84 is there a 95% probability that the difference exceeds the mea­sure­ment error alone.

Once assured that such differences are not a function of mea­sure­ment error, then any changes in growth and body compo­sition can be correlated with factors such as age, the onset of disease, response to nutri­tion inter­vention therapy, and so on.

The collection of longitudinal anthro­pometric data is more time consuming, expensive, and laborious than from cross-sectional surveys, and, as a result, the sample size is generally smaller. Hence, the probability of sys­tem­atic sampling bias (Section 1.4.2) is generally greater than in more extensive cross-sectional surveys.

For cross-sectional studies, the examiners should be rotated among the subjects to reduce the effect of mea­sure­ment bias of the individual examiners. Statistical methods exist for removing anthro­pometric mea­sure­ment error from cross-sectional anthro­pometric data; details are given in Ulijaszek and Lourie (1994).

Cross-sectional surveys are useful for comparing population groups, provided that probability sampling techniques have been used to ensure that the samples are represen­tative of the populations from which they are drawn (Chapter 1). Recently WHO has provided countries with tools to develop or strengthen their surveillance systems so they have the capacity to monitor changes in the Global Nutri­tion Targets for 2030. They include the following anthro­pometric indicators: stunting, wasting, low birthweight, and childhood over­weight. For more details see: WHO Nutrition Tracking Tool.

9.3.3 Errors from changes in tissue compo­sition and properties

Variation in the compo­sition and physical properties of certain tissues may occur in both healthy and diseased subjects, resulting in inaccuracies in certain anthro­pometric mea­sure­ments. Even among healthy individuals, body weight may be affected by variations in tissue hydration with the menstrual cycle (Heymsfield and Casper, 1987; Madden and Smith, 2016).

Skinfold thickness mea­sure­ments may be influenced by variations in compressibility and skin thickness with age, gender, and the level of tissue hydration (Martin et al., 1992; Ward and Anderson, 1993). For example, repeated mea­sure­ments of skinfolds, over a short period (i.e., 5min), may actually decrease accuracy of skinfolds because later mea­sure­ments are more compressed due to the expulsion of water from the adipose tissue at the site of the earlier mea­sure­ment (Ulijaszek and Kerr, 1999).

The accuracy of waist circum­ference is affected by both the phase of respiration at the point of mea­sure­ment and by the tension of the abdominal wall. The phase of respiration is important because it deter­mines the extent of fullness of the lungs and the position of the diaphragm at the time of the mea­sure­ment. Increasing the tension of the abdominal wall (by sucking in) is frequently an unconscious reaction which is also important because it reduces the waist mea­sure­ment. To minimize these errors, WHO (2011) recom­mends advising the subject to relax and take a few deep, natural breaths before the actual mea­sure­ment and at the end of normal expiration.

In addition, during aging, demineral­ization of the bone and changes in body water may result in a decrease in the density of the fat-free mass (Visser et al., 1994; JafariNasabian et al., 2017), which are not always taken into account when calculating total body fat and hence fat-free mass from skinfolds via body density (see Chapter 11 for more details).

9.3.4 Invalid models and errors in body compo­sition

Invalid assumptions may lead to erroneous estimates of body compo­sition when these are derived from anthro­pometric mea­sure­ments, especially in obese or elderly patients and those with protein-energy mal­nu­trition or certain disease states. For instance, use of skinfold thickness mea­sure­ments to estimate total body fat assumes that (a) the thickness of the sub­cu­taneous adipose tissue reflects a constant proportion of the total body fat and (b) the sites selected represent the average thickness of the sub­cu­taneous adipose tissue. In fact, the relationship between sub­cu­taneous and internal fat is nonlinear and varies with body weight, age, and disease state. Very lean subjects have a smaller proportion of body fat deposited sub­cu­taneously than do obese subjects, and in malnourished persons there is probably a shift of fat storage from sub­cu­taneous to deep visceral sites. Variations in the distri­bution of sub­cu­taneous fat also occurs with age, sex, and ethnicity or race (Wagner and Heyward, 2000; He et al., 2002).

Estimates of mid-upper-arm muscle area are used as an index of total body muscle and the fat-free mass (Chapter 11), regardless of age and health status of the subjects. Such estimates are made, despite the known changes in the relationship between arm muscle and fat-free mass with age and certain disease states (Heymsfield and McManus, 1985), and the questionable accuracy of the algorithms used (Martine et al., 1997). Moreover, even the corrected algorithms developed for adults overestimate arm muscle area in obese persons when compared with the deter­mination by computerized tomography (Forbes et al., 1998).

Increasingly, body compo­sition is assessed by laboratory methods; these are described in Chapter 14. Even laboratory methods are based on certain assumptions that have been challenged in recent years. For example, until recently, densitometry, frequently using underwater weighing, has been the gold standard reference method for the deter­mination of the per­cent­age of body fat. The assumptions used in densitometry are that the densities of the fat mass and fat-free mass are constant at 0.90 and 1.10kg/L, respectively (Chapter 11). Several researchers have questioned the validity of using a constant density of the fat-free mass for groups who vary in age, gender, levels of body fatness, and race or ethnicity (Visser et al., 1997). During aging, the density of the fat-free mass may decrease due to demineral­ization of the bone and changes in body water, as noted above (Visser et al., 1994; JafariNasabian et al., 2017), which are not always taken into when calculating total body fat from skinfolds via body density, leading to a 1%–2% overestimate of the body fat content in such subjects (Deurenberg et al., 1989); see Chapter 11 for more details.

In contrast, persons of African descent have a larger fat-free mass because they have a greater bone mineral density and body protein content compared to Caucasians (Wagner and Heyward, 2000). Such differences lead to an underestimate of body fat, when generalized equations developed for Caucasians are used.

Per­cent­age of body fat can also be deter­mined using an isotope dilution technique and dual‑energy X‑ray absorptiometry (DXA) (Chapter 14). Both of these methods assume a constant hydration of the fat-free mass (i.e., 73.2% water content), despite knowledge that it varies with age (Wang et al., 1999), obesity, and pregnancy (Hopkinson et al., 1997), and throughout the course of a clinical condition (e.g., inflammation) (Müller et al., 2016). When the actual hydration of fat-free mass is higher than the assumed value, then the per­cent­age of body fat is underestimated by isotope dilution techniques (Chapter 14) (Deurenberg-Yap et al., 2001). For example, even when pregnancy-specific values for hydration have been applied to account for the increased accretion of water that occurs during pregnancy, individual estimates of fat mass using isotope dilution differed by > 3kg from values based on the four-compartment model (Hopkinson et al., 1997). In contrast, hydration effects on estimates of fat by DXA are not significant (Pietrobelli et al., 1998).

Fortunately, the advent of multicomponent models (i.e., the 4‑compartment-model) with minimal assumptions for assessing body compo­sition circumvent the use of older methods, which use assumptions that are not always valid for certain ethnic groups or the elderly (Müller et al., 2016). Nevertheless, the use of multicomponent models is expensive, requiring more time and facilities.

9.4 Inter­pretation and evaluation of anthro­pometric data

Anthro­pometric indices are derived from two or more raw mea­sure­ments, as noted earlier. Normally, it is these indices that are interpreted and evaluated — not the raw mea­sure­ments. Anthro­pometric indices can be used at both the individual and the population levels to assess nutri­tional status and to screen and assess a response during inter­ventions. In addition, in populations, anthro­pometry can be used to identify the deter­minants and consequences of mal­nu­trition and for nutri­tional surveillance. To achieve these objectives, knowledge of factors that may modify or “condition” the inter­pretation of abnormal anthro­pometric indices is generally required. These conditioning factors are briefly discussed below, together with anthropometric reference data and methods to evaluate anthropometric indices, including classification systems that identify individuals and populations as “at risk” for mal­nu­trition.

9.4.1 Conditioning factors

A variety of factors are known to modify or condition the inter­pretation of anthro­pometric data and must be taken into account. Some important examples include age, birthweight, birth length, gesta­tional age, sex, parental stature, and feeding mode during infancy. Maturation during adolescence, prepregnancy weight, maternal height, parity, smoking, pregnancy, and ethnicity are major conditioning factors for adults (WHO, 1995).

Information on some of these conditioning factors can be obtained by physical examinations, questionnaires, or self-reports. An accurate assessment of age is especially critical for the derivation of many anthro­pometric indices used to identify abnormal anthro­pometry, notably height-for-age and weight-for-age. See: WHO Child Growth Standards.

Age is also important for categorizing the data into the age groups recom­mended by WHO for analysis and inter­pretation (WHO/UNICEF, 2019); see Chapter 13 for details. In more affluent countries, the assessment of age using birth certificates is generally easy, but in some low-income countries, local calendars of special events are often constructed to assist in identi­fying the birth date of a child.

Alternatively, for young children, age is sometimes assessed by counting deciduous teeth. This method is most appro­priate at the population level because of the wide variation among individuals in the timing of deciduous eruption (Delgado et al., 1975). For individuals, bone age can be estimated from the left-hand-wrist radiograph using the Tanner Whitehouse II method (Tanner et al., 1983). Gorstein (1989) has high­lighted the marked discrepancies that may occur in the prevalence estimates of undernutri­tion during infancy when different methods are used to deter­mine age.

With infants, an accurate assessment of birth weight, and, if possible, birth length and gesta­tional age, is also important (Hediger et al., 1999). Assessment of gesta­tional age is especially critical for the inter­pretation of both size-for-age mea­sure­ments during infancy and the neuro­develop­mental progress of preterm infants. It is also essential for the management of pregnancy and the treatment of new-born infants.

Several strategies are available for estimating gesta­tional age. Prenatal measures of gesta­tional age include calculating the number of completed weeks since the beginning of the last menstrual period, prenatal ultra­sonography, and clinical methods; they are all described in Chapter 10. In public health settings, the definition of gesta­tional age on the basis of the last menstrual period is most frequently used, although it is associated with several problems: errors may occur because of irregular menses, bleeding early in pregnancy, and incorrect recall by mothers. Prenatal ultra­sonography during the first or second trimester, although considered the gold standard method for assessment of gesta­tional age, is not universally available, especially in low-income countries. Further­more, the quality of both the equipment used and the technical training varies.

For studies of the adolescent age group, defined by WHO (1995) as 10–19y, information on maturation should also be collected in view of the marked variation in the timing of the maturational changes during adolescence. The best measure of maturity is bone age — often termed skeletal maturation — because it can be obtained for both sexes over a wide age range. However, special equipment and expertise are required for the assessment of bone age. Hence, instead, surrogate measures of somatic maturation are generally used in nutri­tion surveys. 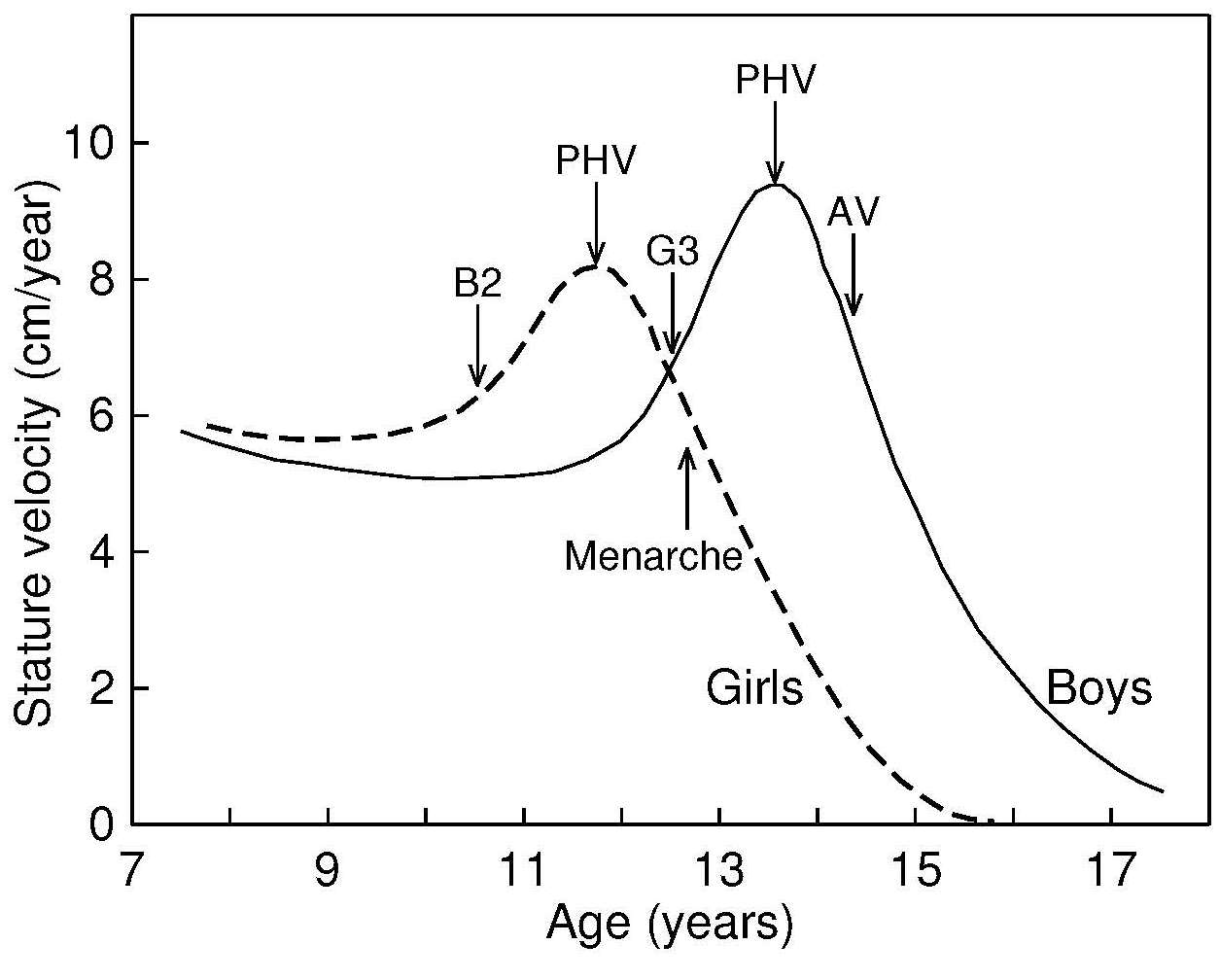WHO (1995) recom­mends the use of two maturational events for each sex to assist in interpreting anthro­pometric data during adolescence: one marker signaling the beginning of the adolescent growth spurt in each sex, and one indicating that the peak velocity for height and associated changes have passed. In girls, the indicator that can be used to signal that the adolescent growth spurt has begun is the start of breast development, which precedes peak height velocity by about 1y. The marker indicating that most of the adolescent growth spurt has been completed is the attainment of menarche, which begins a little more than 1y after peak height velocity (Figure 9.1). In boys, the corresponding indicators signaling the beginning and completion of the adolescent growth spurt are adolescent changes in the penis, characterizing G3, followed by the attainment of adult voice, respectively (Figure 9.1).

When an assessment of somatic maturation cannot be obtained by physical examination and questioning, then a self-administered questionnaire containing drawings illustrating Tanner's stages of development of breasts and pubic hair for females, or pubic hair and male genitalia, may be used. Adolescents are requested to select the drawing closest to their stage of development, as described in Morris and Udry (1980).

9.4.2 Appro­priate anthropometric reference data

In public health settings, appro­priate anthro­pometric reference data facilitate international comparisons of anthro­pometric indices across populations and enable the proportion of individuals with abnormal indices to be deter­mined relative to the reference population. Such comparisons enable the extent and severity of mal­nu­trition in the study group to be estimated. In surveillance studies, reference data allow the evaluation of trends over time, as well as the effectiveness of inter­vention programs to be assessed. Reference data can also be used in clinical settings to monitor growth of individuals, detect abnormal changes in growth, and assess response to treatment (WHO, 1995).

The WHO recom­mends the use of the WHO Child Growth Standards for young children from birth to 5y for international use (WHO, 2006) in view of the small effect of ethnic and genetic differences on the growth of infants and young children compared with the environmental, nutri­tional, and socio-economic effects, some of which may persist across generations. The WHO Child Growth Standard was developed as a result of the technical and biological limitations identified with the earlier NCHS/WHO growth reference (Garza and de Onis, 1999). A prescriptive approach depicting physiological human growth under optimal conditions was used for the new Child Growth Standards so they represent how young children should grow, rather than as a “reference” describing how children do grow. To achieve this goal, a set of individual eligibility criteria were developed: term singleton infants with non-smoking mothers, a health status that did not constrain growth, and mothers who were willing to follow current WHO feeding recom­mendations. The design combined a longitudinal study from birth to 24mos with a cross-sectional study of children aged 18–71mos based on pooled data from 6 participating countries (Brazil, Ghana, India, Norway, Oman, and the United States) (de Onis et al., 2004). WHO has developed a tool for the application of the WHO Child Growth Standards which includes instructions on how to take the mea­sure­ments, interpret growth indicators, investigate causes of growth problems, and how to counsel caregivers. An anthro­pometry training video is also available. For more details, see: WHO Child Growth Training Module.

For older children, the WHO growth reference data for school-age children and adolescents 5–19y should be used (de Onis et al., 2007). This is a reconstruction of the original 1977 National Centre for Health Statistics (NCHS) data set supplemented with data from the WHO Child Growth Standard. The statistical methodology used to construct this reference was the same as that used for the WHO Child Growth Standard.

A series of prescriptive standards for monitoring fetal, newborn growth, and gesta­tional weight gain have also been developed for international use by the INTERGROWTH‑21^st project. This project adhered to the WHO recom­mendations for assessing human size and growth, and followed healthy pregnant women longitudinally from 9wks of fetal life to 2y (Papageorghiou et al., 2018; Ismail et al., 2016). Populations from urban areas of 8 countries in which maternal health care and nutri­tional needs were met (Brazil, China, India, Italy, Kenya, Oman, the UK and the USA) were involved to ensure universal multi-ethnic growth standards were generated that represent how fetuses should grow. Postnatal growth standards for preterm infants were also developed by this group (Villar et al., 2015).

Updated childhood growth charts have been prepared by the Center for Disease Control (CDC) for U.S children for two age groups: 0–36mos and 2–20y. These CDC 2000 growth charts are based primarily on physical measure­ments taken during five nationally represen­tative surveys conducted between 1963 and 1994, although some supplemental data were also used. When creating these revised growth charts, two data sets were excluded: growth data for very low birthweight infants (< 1500g) whose growth differs from that of normal birth-weight infants, and weight data for children > 6y who participated in the NHANES III survey. The latter data were excluded from both the revised weight and BMI growth charts because their inclusion shifted the upper per­cen­tile curves. Hence, the exclusion of these selected data resulted in a modified growth reference that is not a purely descriptive growth reference because it does not contain represen­tative national data for all variables (Kuczmarski et al., 2000). A comparison of these CDC 2000 Growth Charts with the WHO Child Growth Standards is available in de Onis et al. (2007).

For body compo­sition indices, use of local reference data are preferred because racial differences exist in both body proportions, and the amount and distri­bution of sub­cu­taneous and intra-abdominal fat (Wagner and Heyward, 2000; He et al., 2002; Lim et al., 2019). In practice, however, only a few countries have local body compo­sition reference data. In the absence of such local data, WHO recom­mend the use of the reference data for mid-upper-arm circum­ference (MUAC), triceps and subscapular skinfolds based on the data collected during the WHO MGRS on children age 0–5y. Electronic copies of the WHO tables and charts of per­cen­tiles and Z‑scores for MUAC‑for-age, triceps-for-age, and subscapular-for age by sex are available for children from age 3mos to 71mos and are included in WHO Child Growth Standards.

In clinical settings, abnormal changes in the rate of growth of a child can be detected much earlier when growth velocity charts, rather than distance growth charts, are used; see Chapter 13 for more details. Growth velocity charts are based on longitudinal studies during which the same child is measured serially, and the growth rate calculated for each interval. WHO has developed a set of growth velocity charts based on the WHO MGRS described earlier for international use; see de Onis et al. (2011) for more details.

Several different distance growth standards have been compiled, depending on the specific deter­minants of growth. For example, the new international postnatal growth standards should be used for preterm infants (Villar et al., 2015) in view of the difference in weight, length, and head circum­ference between preterm and full-term infants. More­over, the time period over which these differences extend varies with the growth mea­sure­ment. Differences are significant until 18 mos for head circum­ference, until 24mos for weight-for-age, and up to 3.5y for length/height-for-age.

Alternatively, tempo-conditional growth charts can be used for monitoring the growth of individual children during adolescence (Figure 9.2).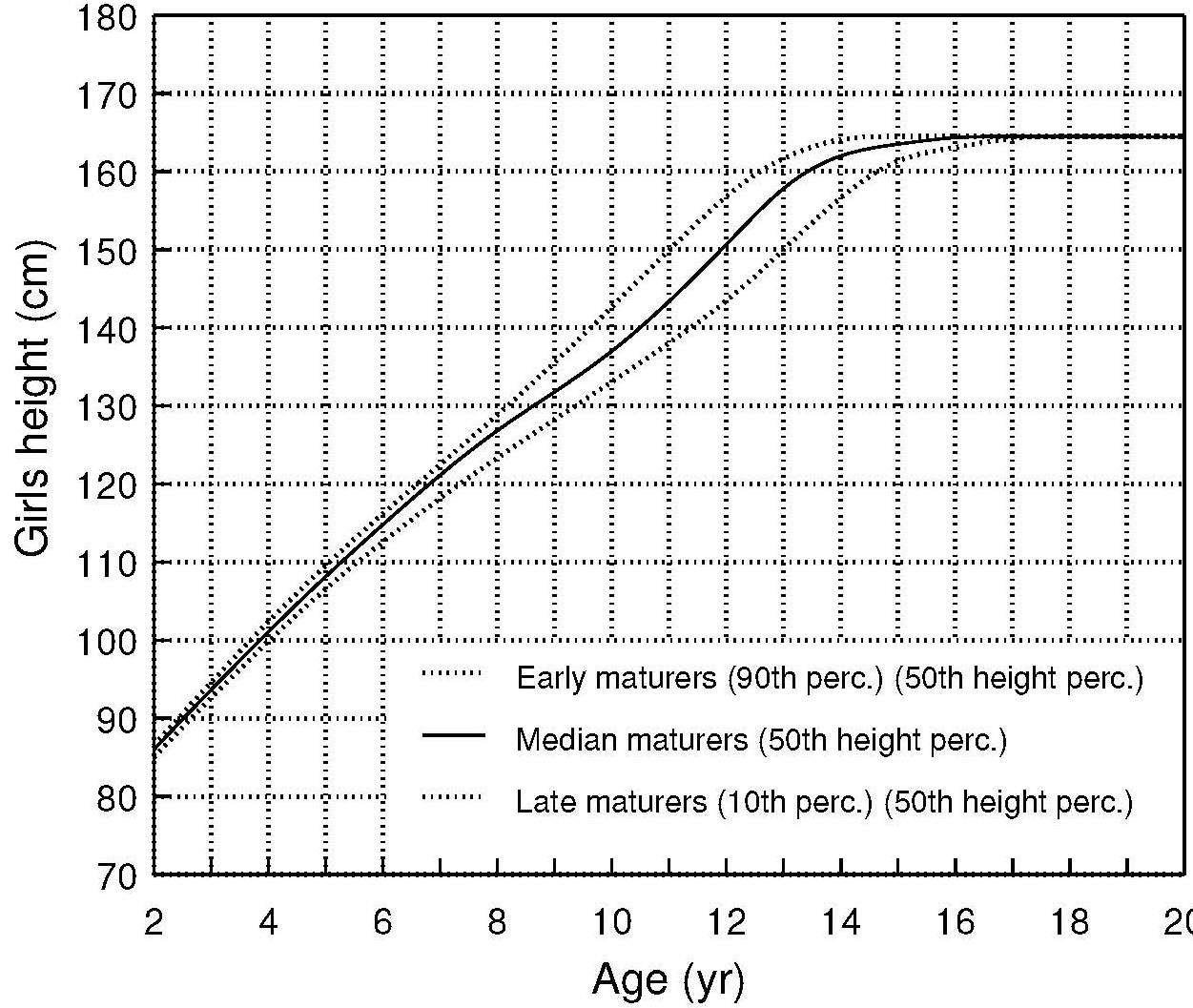

These growth charts are based on mixed cross-sectional and longitudinal data, and take into account differences in the timing of the adolescent growth spurt — termed the “phase difference effect” (Tanner & Buckler, 1997).

Parent-allowed-for growth reference data are available for children from 2–9y when nonfamilial short stature is of concern. Cole (2000) developed a novel parent-allowed-for-height chart that adjusts for mid-parent, single parent, or sibling height based on the UK90-height reference. Special growth charts have also been compiled for children with certain genetic disorders such as Down's syndrome or other developmental disorders in which growth patterns differ from the reference growth curves.

9.4.3 Methods of evaluating anthropometric indices

For studies of both individuals and populations, the anthro­pometric indices can be compared to the reference population using per­cen­tiles or Z‑scores derived from the distri­bution of the anthropometric reference data. A per­cen­tile refers to the position of the mea­sure­ment value in relation to all the mea­sure­ments for the reference population, ranked in order of magni­tude. A Z‑score (or standard deviation score) measures the deviation of the value for an individual from the median value of the reference population, divided by the standard deviation of the reference, as shown below: \[\small \mbox{Z‑score or SD score = } \frac {\mbox {(observed value) − (median reference value)}}{\mbox {(standard deviation of reference population)}}\] In most industrialized countries, per­cen­tiles are used because no errors are introduced if the data have a skewed distri­bution. Weight-for-age, weight-for-height, and many circumferential and skinfold indices have skewed distri­butions.

per­cen­tiles are not appro­priate for use in low- and middle-income countries (LMICs) where many children may fall below the lowest per­cen­tile.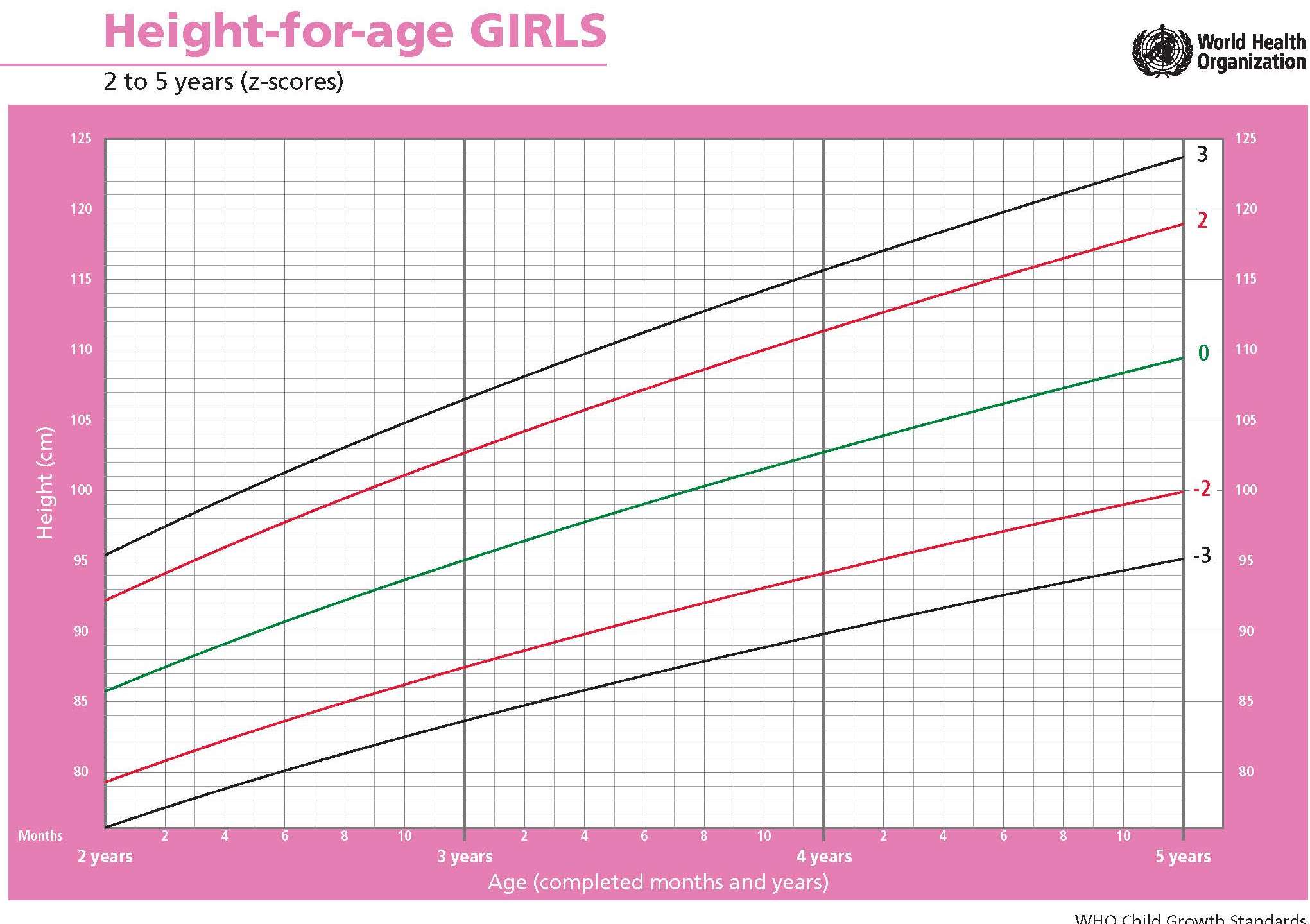

In these settings Z‑scores should be used because they can be calculated accurately beyond the limits of the original reference data. Hence, individuals with indices below the extreme per­cen­tiles of the reference data can then be classified accurately. For more discussion of per­cen­tiles and Z‑scores, see Chapter 13. Both per­cen­tiles and Z‑scores based on the WHO Child Growth Standards (0-5y) and the WHO Growth Reference for school-aged children and adolescents (5-19y) can be readily calculated in population studies using the WHO software program: WHO AnthroPlus (2009). Alternatively, for individuals in clinical settings, the per­cen­tile or Z‑score range within which the mea­sure­ment of an individual falls can be read from sex-specific charts or tables of the appro­priate reference data, as shown in Figure 9.3.

Three methods have been recom­mended by WHO to evaluate cross-sectional anthro­pometric data for use in public health; these are summarized in Box 9.4.

Figure 9.4

is an example of the first method summarized in Box 9.4. Here the frequency distri­bution of the Z‑scores for height-for-age children from the Indian National Family Health Survey (2005-2006) are compared with the corresponding reference distri­bution of height-for-age Z‑scores for the WHO Child Growth Standards. The figure high­lights that nearly all the children surveyed were affected by some degree of linear growth retardation and would benefit from an inter­vention; this approach is termed a “population approach to targeting”.

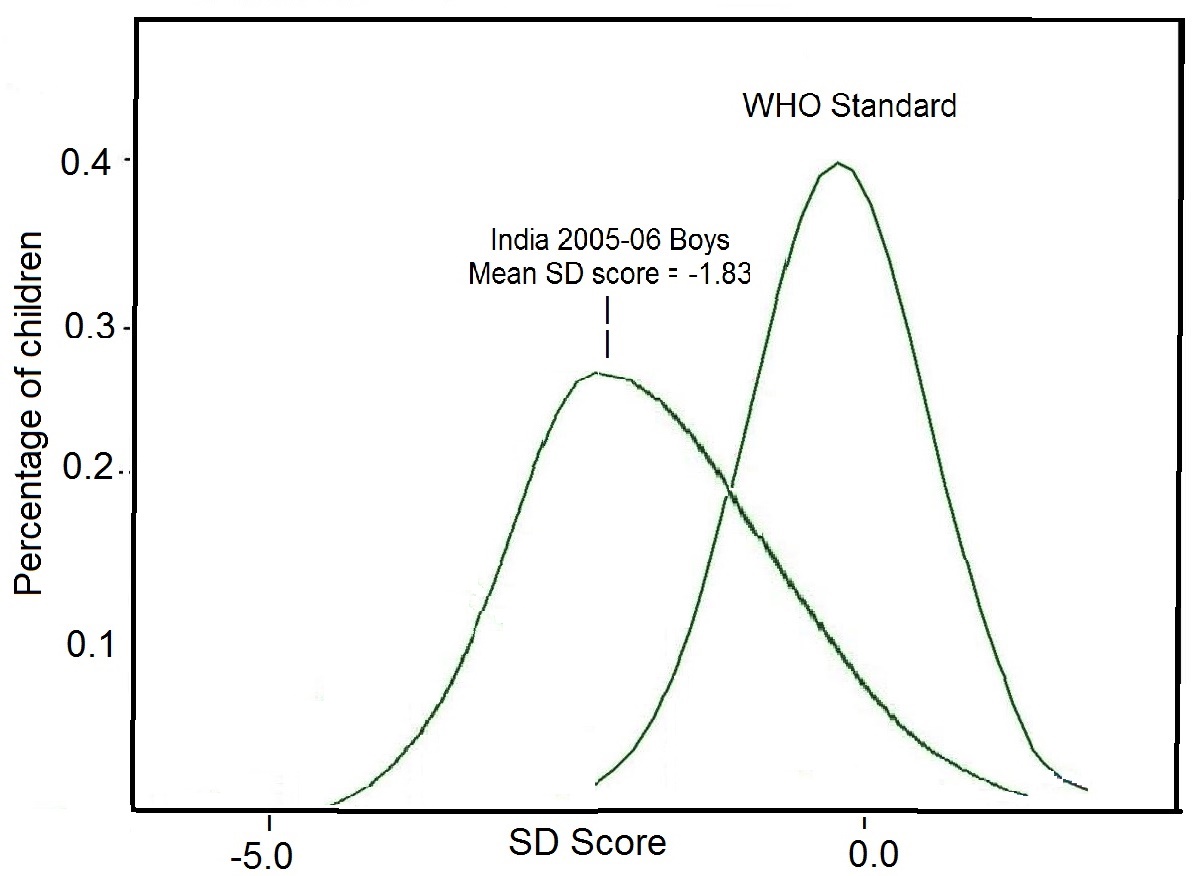
Summary statistics can also be used when anthro­pometric indices are expressed as Z‑scores in population studies. In the example given in Figure 9.4, the calculated mean height-for-age Z‑score (-1.83) for the children was markedly lower than zero — the expected value for the reference distri­bution. This statistic alone indicates that the entire distri­bution has shifted downward, suggesting that most, if not all of the individuals, are affected by linear growth retardation, as was clear from the frequency distri­bution of the height-for-age Z‑scores compared with the corresponding reference distri­bution depicted, in Figure 9.4.

Note, summary statistics cannot be calculated in this way for data from a population expressed in terms of per­cen­tiles which are often not normally distributed.

Alternatively, calculation of the mean Z‑score and SD can be used to compare directly different populations or the status of the same population at different times (Goldstein and Tanner, (1980). However, even if the populations have the same mean Z‑score, their SDs may differ, with the population with the larger SD having a greater proportion below the reference limit or cutoff point, as shown in (Figure 9.5). Here, the growth reference is not being used for comparative purposes as shown in Figure 9.4.

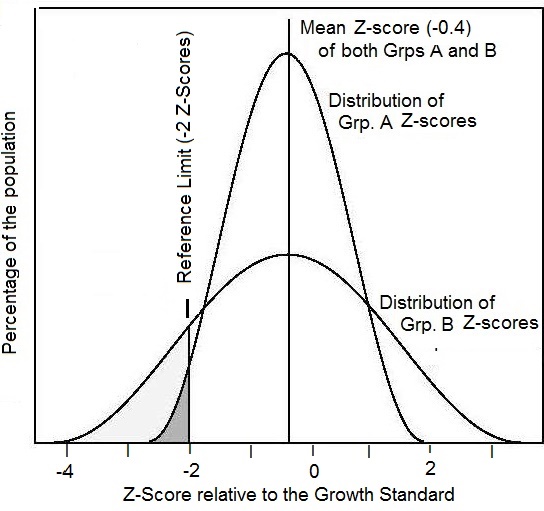
The third method itemized in Box 9.4 involves calculating the per­cent­age of individuals with anthro­pometric indices below or above predeter­mined reference limits or cutoff points. When used in this way, the anthro­pometric index and its associated reference limit or cutoff point are termed an “indicator” as described earlier. This approach is used to classify individuals as “at risk” to mal­nu­trition and is used by governments and International Agencies (e.g., WHO and UNICEF) to generate prevalence estimates of malnutrition for information and comparisons across countries, as well as for advocacy. The approach is described in more detail below.

9.4.4 Classification systems

Classification systems are used in both clinical settings and in public health. All use at least one anthro­pometric mea­sure­ment and one or more reference limit derived from appro­priate reference data (i.e., indicator) to classify at risk individuals. Alternatively, cut-off points are used. In practice, classification schemes are not perfect, some misclassification will always occur so that some individuals identified as “at risk” to mal­nu­trition will not be truly malnourished (false positives), and others classified as “not at risk” to mal­nu­trition will in fact be malnourished (false negatives). Misclassification arises because there is always biological variation among individuals (and hence in the normal levels defined by the mea­sure­ment) (Fraser, 2004); see Chapter 13 for more details.

Reference limits for anthro­pometric indices are derived from a reference distri­bution and can be expressed in terms of Z‑scores or per­cen­tiles. In low income countries reference limits defined by Z‑scores are frequently applied, with scores below −2 or above +2 Z‑scores of the WHO Child Growth Standard or WHO Growth Reference used to designate individuals with either unusually low or unusually high anthro­pometric indices (WHO, 1995). This approach is used because statistically 95% of the international reference population fall within the central range assumed to be “healthy”. Therore, theoretically, the proportion of children with a Z‑score less than −2 or greater than +2 in a study population should be ≈ 2.3%. Clearly, if the proportion in the study population with such low or high Z‑scores is significantly greater than this, then the study population is seriously affected. The WHO uses the below −2 Z‑scores of the WHO reference median for weight-for-age, length/height-for-age, or weight-for-height to classify children as under­weight, stunted, or wasted, respectively.

In industrialized countries, the per­cen­tiles commonly used for designating individuals as “at risk” to mal­nu­trition are either below the 3^rd or 5^th and above the 97^th or 95^th per­cen­tiles. The limits chosen depend on the reference data used: see Chapter 13 for more details.

There is nothing immutable about a reference limit at −2 Z‑score, despite their use by countries and agencies to generate prevalence estimates, most notably for stunting and wasting. As a consequence, attempts have been made to establish “cutoffs” for some anthropometric indicators to improve the ability to discriminate between children who are malnourished and those who are “healthy”. These cutoffs have been established by a review of the anthro­pometric characteristics of individuals with either clinically moderate or severe mal­nu­trition or who subsequently die. However, many other characteristics of individuals such as age, sex, life-stage, race/ethnicity, genetics, and morbidity or nutri­tional status may affect the relationship under study (Hondru et al., 2019; Yaghootkar et al., 2020; Wright et al., 2021). Hence, in practice, defining cutoffs is difficult because the relationship between the indices and the biological factors cannot be generalized from one region to another (WHO Expert Consultation, 2004).. Consequently, in some studies universal cutoff points are used, whereas in others the methods used to identify the cutoff points applied are not always well documented.

As an example in a study of low BMI and morbidity in Pakistan, a reported a cutoff of < 18.5 was associated with higher morbidity, whereas in Calcutta it was < 16.0 (Campbell and Ulijaszek, 1994; Kennedy and Garcia, 1994).

Cut-offs for BMI, waist circum­ference, and waist-hip ratio associated with risk of cardiovascular disease and type 2 diabetes have also been extensively investigated among different ethnic groups (Ding et al., 2020; WHO Expert Consultation, 2004; Lear et al., 2010). Some expert groups have defined lower waist circumference cutoffs for adults of Asian descent compared to Europeans (IDF, 2006).

Receiver operating characteristic (ROC) curves are often used to deter­mine cutoff points. This is a graphical method of comparing indices and portraying the trade-offs that occur in the sensitivity and specificity of a mea­sure­ment or index when the cutoffs are altered. To use this approach, a spectrum of cutoffs over the observed range of the indicator results is used, and the sensitivity and specificity for each cutoff calculated. Next, the sensitivity (or true-positive) rate is plotted on the vertical axis against the true negative rate (1−specificity) on the horizontal axis for each cutoff point, as shown in (Figure 9.6).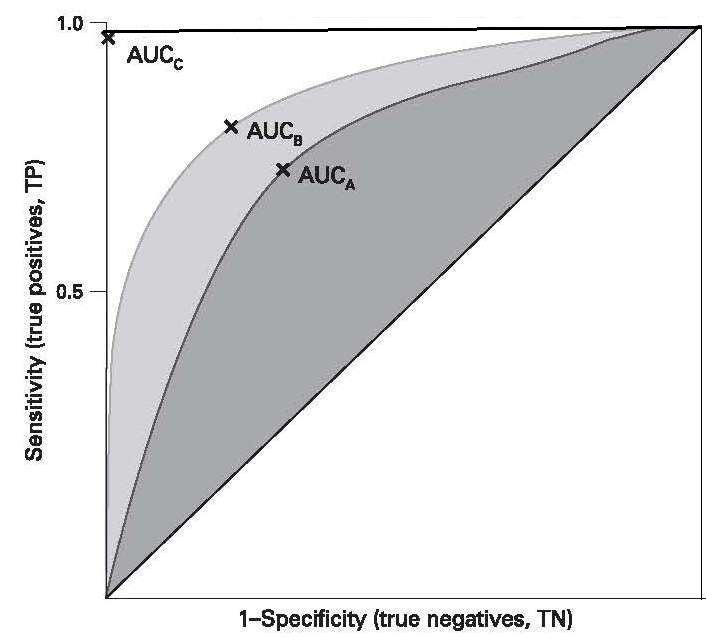

The closer the curve follows the left-hand of the ROC space, the more accurate is the cutoff under study in distinguishing the health or nutri­tional status condition under investigation from optimal status. The optimal ROC curve is the line connecting the points highest and farthest to the left of the upper corner. The closer the curve comes to the 45° diagonal of the ROC space, the less accurate the indicator cutoffs (Søreide, 2009). Most statistical programs (e.g., SPSS) provide ROC curve analysis. Details of alternative statistical methods for selecting the best cutoff point are given in Brownie et al. (1986).

The choice of the cutoff may vary depending on the circumstances. When resources are scarce, a low cutoff point may be selected. As a consequence, the sensitivity decreases, which mean that more truly malnourished children are missed. However, at the same time, the specificity increases, which means that fewer well-nourished children are misdiagnosed as malnourished. Conversely, when resources are generous, the cutoff can be high, because it does not matter if some children receive treatment when they do not need it. The inverse relationship between sensitivity and specificity and relative risk of mortality associated with various values for MUAC in children 6–36mos in rural Bangladesh is shown in Table 9.4.

Table 9.4. Sensitivity, specificity, and relative risk of death associated with various values for mid-upper-arm circumference in children 6–36mos in rural Bangladesh. Data from Briend et al. (1987).

Arm circum- ference (mm)	Sensitivity (%)	Specificity (%)	Relative Risk of death
≤ 100	42	99	48
100–110	56	94	20
110–120	77	77	11
120–130	90	40	6

More details of the inter-relationships between these variables is given in Chapter 1.

Unfortunately, because sensitivity and specificity data for the anthro­pometric indices selected are usually not known for the population under study, the data required to plot ROC curves are often obtained elsewhere, even though the values may not be appro­priate for the population under study because of the many factors known to influence cutoff values, as noted earlier; see Chapter 13 for more details. Ultimately the choice of an index and an associated cutoff point (i.e., an indicator) depends on the resources available and the purpose for which it is being used. The latter can range from screening for disease or monitoring to detect changes in prevalence of mal­nu­trition etc. For more discussion on the selection of anthro­pometric indicators, see Brownie et al. (1986) and WHO (1995).

Screening tools to identify those who are malnourished in clinical or public health settings can be based on single or multiple mea­sure­ments and associated reference limits or cutoff points. An example of a screening tool used in clinical settings is the Mal­nu­trition Universal Screening Tool (MUST), widely used to identify adults who are at risk of undernutri­tion or obesity (See Chapter 27). MUST is based on height and weight mea­sure­ments from which both a BMI score (from 3 cutoffs) assessed via a chart and weight loss in previous 3–6mos, can be derived, followed by establishing acute disease effect and score. From the sum of the three scores, the overall risk of mal­nu­trition is calculated, with management guidelines provided according to the level of risk (low; medium; high). More details are available: Mal­nu­trition Universal Screening Tool .

In public health emergencies, a screening tool based on a single mea­sure­ment (i.e., MUAC) and associated cutoff (i.e., < 115mm) is often used to identify severe acute mal­nu­trition (SAM) in children 6–60mos. This MUAC cutoff was chosen because children with a MUAC < 115mm were observed to have a highly elevated risk of death compared to those with a MUAC > 115mm (Myatt et al., 2006).

For defining over­weight and obesity in children and adolescents, WHO recom­mends the use of BMI-for-age Z‑scores and reference limits based on Z‑scores. For children (0–5y), a Z‑score for BMI-for-age above +1 is described as being “at risk of over­weight”, above +2 as “over­weight”, and above +3 as “obese” based on the WHO Child Growth Standard. For children 5–19y, BMI-for-age Z‑scores above +1 and above +2 based on the WHO 2007 growth reference data are recom­mended (de Onis & Lobstein, 2010). To classify over­weight and obesity in adults, however, WHO recom­mends a graded classification scheme, as shown in (Table 9.5).

Table 9.5. WHO classification of obesity in adults according to body mass index (BMI). From: WHO (2000).

Classification	BMI (kg/m2)	Risk of comorbidities
Under­weight	< 18.50	Low (but risk of clinical problems is increased)
Normal range	18.50–24.99	Average
Over­weight	≥ 25.00
Pre-obese	25.00–29.99	Increased
Obese class I	30.00–34.99	Moderate
Obese class II	35.00–39.99	Severe
Obese class III	≥ 40.00	Very severe

Increasingly, it is recognized that in low-income countries, multiple anthropometric deficits may occur simultaneously in children and amplify their risk of morbidity and mortality. Consequently, a composite index of anthropometric failure (CIAF) has been developed, and is described in Chapter 13.

In public health, screening tools are also used to map countries according to levels of severity of mal­nu­trition (UNICEF/WHO/World Bank, 2021) in order to identify priority countries. Five prevalence thresholds (as %) based wasting (i.e., WHZ < −2), over­weight (BMIZ > +2), and stunting (i.e., HAZ < −2) have been developed by WHO and UNICEF; these are depicted in (Table 9.6). The fifth threshold labelled “very low” and of no public health concern was included across all three indicators to reflect the expected prevalence of 2.3% (rounded to 2.5%) below/above 2 SDs from the median of the WHO Child Growth Standard.

Table 9.6. Prevalence thresholds, corresponding labels, and the number of countries (n) in different preva­lence threshold categories for wasting, over­weight and stunting in children under 5y using the “novel approach”. From: de Onis et al. (2018).

Wasting			Over­weight			Stunting
Prevalence thresholds (%)	Labels	(n)	Prevalence thresholds (%)	Labels	(n)	Prevalence thresholds (%)	Labels	(n)
< 2·5	Very low	36	< 2·5	Very low	18	< 2·5	Very low	4
2·5 – < 5	Low	33	2·5 – < 5	Low	33	2·5 – < 10	Low	26
5 – < 10	Medium	39	5 – < 10	Medium	50	10 – < 20	Medium	30
10 – < 15	High	14	10 – < 15	High	18	20 – < 30	High	30
≥ 15	Very high	10	≥ 15	Very high	9	≥ 30	Very high	44

The number of countries in different threshold categories for wasting, over­weight, and stunting, also shown in (Table 9.6), is based on data from 134 countries. Comparison of the prevalence estimates for each anthro­pometric indicator can trigger countries to identify the most appro­priate inter­vention program to achieve “low” or “very low” prevalence thresholds.

Details of the techniques used to measure body size and body compo­sition, together with the indices derived from these mea­sure­ments, are discussed in Chapters 10 and 11, whereas Chapter 13 discusses methods used for evaluation of anthro­pometric indices and their application at the individual and population level.